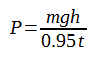今回はいよいよ走行中の自転車について物理モデルを考え、GPSログからパワーを見積もる方法について解説します。実はすでにこれをやった方もいて、下のページで詳しく説明されています。
実際の計算にあたってはこのサイトの情報を参考にさせていただきました。ただ何でも自分で確かめないと気が済まない人ですので(笑)、すべて自力で計算して検証してみました。
初めてたどり着いた方は下の基礎編も合わせてお読みいただければ幸いです。
物理モデル
GPSログからパワーを求めるために、簡略化された物理モデルを考えます。下の図はGPSログの隣接する2点間における断面図であるとします。実際には時間にして数秒~十数秒、距離にして数メートルから数十メートルくらいのごく短い区間です。もちろん平坦な道もあれば上り坂も下り坂もあるわけですが、一般的には上り坂を考えておけば、平坦区間では傾斜をゼロ、下り坂では傾斜をマイナスとすればいいだけの話です。

前提条件
まずこの短い区間では自転車に働いている力は一定であるとします。力はGPSログの加速度から求められますが、これ以上細かい変化は知りようがないからです。したがって、この区間内では等加速度運動をしているものと仮定します。
またこの短い区間内では傾斜の変化もないものとします。やはりGPSログからはそれより細かい高度の変化は知りようがないからです。したがって自転車は道路に沿った直線上を運動するものとし、この直線上にx軸をとります。
GPSログの隣接する2点間のうち、時刻の早い方をt=0、時刻の遅い方をt=Tとします。この間の時間差は当然Tです。
時刻tの瞬間に自転車がいる位置をxで表します。xは時間の関数ですからx(t)と書けます。t=0の瞬間にはx=0、t=Tの瞬間にはx=Dにいるものとします。したがって2点間の距離はDとなります。なおDはGPSログから求められる既知量です。
自転車が走行する速度をvとします。ここでは等加速度運動を考えていますので速度も時間とともに変化し、v(t)と書くことができます。時刻t=0の瞬間の速度をv=v0、時刻t=Tの瞬間の速度をv=v1とします。
2点間の標高差をhとします。また路面の傾斜を仮にθとします。GPSログから直接求められるのはhの方ですが、θはhと次の関係が成り立ちます。
sinθ=h/D
加速度
区間の両端における速度v0, v1はGPSログから既知量ですから、加速度aは次の式によって求められます。
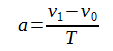
速度
時刻tにおける速度は加速度を時間で積分することによって得られます。
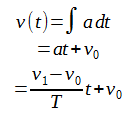
つまりv(t)はtの1次関数であり、v0からv1まで直線的に変化します。
速度と距離の関係
時刻tが0からTまで変化する間に進む距離はDであることがわかっていますが、これを速度と結びつけるには速度を時間で積分すれば得られます。
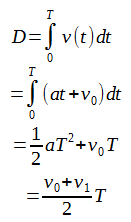
つまり距離Dは両端における速度v0, v1の平均値に時間差Tを掛けたものに等しくなります。
自転車に働いている力
走行中の自転車に働いている力には、大きく分けるとライダーがペダルに加えた力(推進力)とそれを邪魔しようとする力(抵抗力)に分かれます。ここでは自転車を前に進めようとする力をFとし、これを求めることが目的になります。
一方、自転車を後ろへ引っ張ろうとする力には大きく分けて3通りあり、重力抵抗(Fg)と空気抵抗(Fa)と転がり抵抗(Fr)に分かれます。これらはすべて進行方向と逆向きに働く力ですから、符号としてはマイナスになります。これらについて詳しく見ていきましょう。
1. 重力抵抗
ライダーの体重と自転車を含めた全重量をm、重力加速度をgとすると、地球の中心に向かって働く重力はよく知られているようにmgとなります。この重力のうち、路面と平行な方向に働く分力Fgは傾斜θを使って次のように書けます。
Fg=mg・sinθ
ここで平地ではθ=0ですから、当然Fg=0となります。また下り坂ではθがマイナスとなるため、sinθもマイナスとなり、Fgの符号が反転します。したがって、下り坂では抵抗ではなく自転車を前に進めようとする力に変わるわけです。
2. 空気抵抗
一番ややこしいのはこの空気抵抗です。上り坂ではさほど大きな影響はありませんが、平地では最も大きな抵抗力として働きます。空気抵抗を厳密に見積もるには流体力学的な考察が必要になりますが、ここでは簡略化されたモデルとして先に紹介したサイトの式を使わせてもらうことにします。それも元は「ロードバイクの科学」という本が出典らしいですが、そのうち買って読んでみたいと思います(笑)。
引用元によりますと、空気抵抗Faはライダーの体重(kg)と身長(cm)から次の式で求められます。
Fa=g×0.00007638×体重0.425×身長0.725×ポジション補正係数×空気密度補正係数×速度2
ややこしそうな指数関数が出てきますが、関数電卓があれば計算できます。ここでやっていることは、おそらくライダーの体型から近似的に断面積を割り出しているのだろうと思います。
またポジション補正係数というのは乗車姿勢による空気抵抗の違いを補正するための係数です。下ハンドルを握ったときを1とし、ブラケットポジションでは1.25とするなど、ポジションによって推奨値が示されています。
そしてもう一つ複雑なのは、空気抵抗は標高によっても変化するということです。よく知られているように、標高が上がるにつれて空気は薄くなります。つまり空気密度が低くなるため、その分空気抵抗も減少します。この理論についてはこちらのページで解説されていますが、標高0mでの空気密度をρ0とすると、標高h(m)での空気密度ρ(h)は次の式で近似できます。
ρ(h)=ρ0・e-0.000118・h
ここでeは自然対数の底です。したがって最終的な空気抵抗は、空気密度補正係数としてρ(h)/ρ0を掛けたものになります。たとえば標高2000mでは空気密度は標高0mのおよそ0.8倍になります。
こうやって見ると非常に複雑そうですが、ここで大事なのは空気抵抗は速度の2乗に比例するということです。区間内で係数は変化しませんから、すべての係数をkとしてまとめてやれば、空気抵抗は次のように単純に書くことができます。
Fg = k・v2
したがって、たとえば15km/hに比べて30km/hで走るには4倍もの力が必要になるわけです。
3. 転がり抵抗
転がり抵抗はタイヤと路面との摩擦によって生じる抵抗力です。これは路面に垂直な方向の重力mg・cosθに比例します。やはり先のサイトから引用させてもらうと、転がり抵抗Frは次の式で表すことができます。
Fr=0.00421・mg・cosθ=0.00421・mg・cos(arcsin(h/D))
ここでθはh/Dの逆正弦から求められます。また0.00421はタイヤの転がり抵抗係数と呼ばれますが、当然タイヤによっても異なります。ここでは一般的なロードバイク用タイヤの値を使っているようです。厳密にはタイヤによる実測値を適用する必要がありますが、転がり抵抗は重力抵抗や空気抵抗に比べるとはるかに小さいため、大ざっぱな値でも大きな影響はないようです。
運動方程式
以上で自転車に働いている力がすべてわかりましたので、ニュートンの運動方程式「力=質量×加速度」に当てはめてみます。ここで求めたいのはライダーが加えた推進力Fであり、すべての抵抗力はそれとは逆向きに働くことに注意して運動方程式を立てると次のようになります。
F-Fg-Fa-Fr=ma
ここでmaおよびFg, Fa, FrはGPSログから計算できる既知量ですので、Fを求めることは可能なわけです。もし推進力Fがすべての抵抗力Fg+Fa+Frと釣り合っていれば右辺は0になりますから、加速度がゼロ、すなわち自転車は一定速度で走り続けるわけです。もしFが抵抗力より勝っていれば右辺はプラスになりますから自転車は加速し、Fが抵抗力に負けていれば右辺はマイナスとなって自転車は減速することになります。
引用元での計算は実は右辺がゼロのケースに該当します。つまり等速運動です。おそらくヒルクライムのようにほぼ一定の速度で上り続けることを想定しているのでしょうから、その限りにおいて平均値としては正しいと考えられますね。しかし瞬間的な速度の変化まで考慮に入れると、右辺の加速度を加味しなければなりません。これは特に上り坂よりも平地で大きな影響を及ぼします。なぜなら加速するときに最も大きなエネルギーが必要だからです。
駆動系の伝達損失
実はここまでの議論で考慮していなかった抵抗がもう一つあります。それは自転車自身の駆動系によって生じる伝達損失です。どんな機械でも効率が100%ということはあり得ず、必ずいくらかの損失を伴います。自転車の場合、具体的にはBB、ハブ、チェーンなどの摩擦によって生じる損失がそれに該当します。ですからライダーが加えた力がすべて推進力に変わるわけではなく、いくらかは駆動系自体によってロスしているわけです。
伝達損失も当然パーツのグレードなどによって変わってきますが、一般的なロードバイクではおよそ5%程度であるとされています。逆に言えば効率は95%であるということです。したがって、ライダーが加えた力Fのうち、0.95倍が有効な推進力に変わると考えられます。これに基づいて運動方程式を修正すると次のようになります。
0.95F-Fg-Fa-Fr=ma
ここで求めたいのはライダーが加えた力Fですから、最終的には次の式で求められることになります。
F=(ma+Fg+Fa+Fr)/0.95
以下、この伝達損失は無視して考え、最終的に0.95で割ることによって補正するものとします。
仕事を求める
仕事の定義より、ライダーが行った仕事は「力×距離」で求めることができます。これは数学的に言えば力Fを位置xで積分することと等価です。したがって、ライダーが行った仕事をWとすると、次の式で求められます。
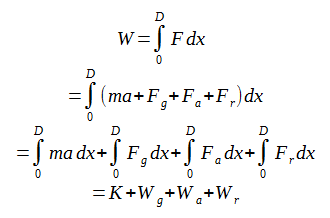
ここで便宜的に各項を運動エネルギーK、重力による仕事Wg、空気抵抗による仕事Wa、転がり抵抗による仕事Wrに分け、それぞれについて計算してみます。
運動エネルギー
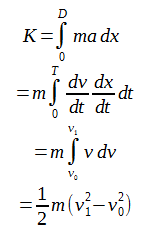
これはよく知られているように、運動エネルギーの増加分になります。自転車が加速するときはライダーがそれだけの仕事をしていることになります。もしv1=v0であればこの項はゼロとなります。またv1<v0であればマイナスとなり、運動エネルギーを失ったことになります。ブレーキをかけた時などはこの項が大きなマイナスを示します。
重力による仕事
重力抵抗は区間内で一定と仮定しますから、Fgに移動距離Dを掛けて
Wg=mg・sinθ・D
と表すことができます。ところがsinθ=h/Dですから、この式は結局
Wg=mgh
というシンプルな形になります。つまりθは完全に消えてしまいました。ということは重力による仕事は傾斜には全く無関係で標高差だけによって決まるということになります。このことは非常に重要なポイントです。
空気抵抗による仕事
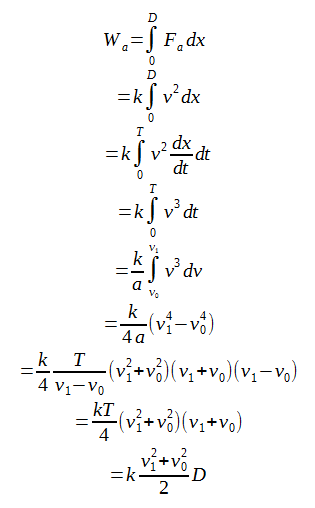
この式を導くのにえらい苦労しましたけど(笑)、結果は非常にシンプルで、速度の2乗の平均に距離を掛けただけであることがわかります。もし加速度がゼロであればv1=v0ですから、単純にWa=kv02Dということになり、確かに合っています。
転がり抵抗による仕事
これは傾斜と全重量だけによって決まる量で区間内で一定ですから、単純にFrに距離Dを掛けるだけです。
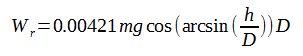
全仕事
最終的にライダーが行った全ての仕事はこれらの和であり、
W=K+Wg+Wa+Wr
となります。この中でWaとWrは常にプラスの量ですが、KとWgはマイナスになる可能性があります。自転車が減速しているときはKはマイナスであり、下り坂ではWgがマイナスとなります。したがって、それらのバランスでWがマイナスになることもあり得ます。たとえば平地でペダルを止めていれば空気抵抗によって次第に減速するのでKはマイナスになりますし、下り坂ではWgが大きなマイナスになります。もしWがマイナスになればライダーはペダルを止めていると考えられますから、仕事はゼロとするのが適当でしょう。
パワー
パワーというのは単位時間あたりの仕事量ですから、上で求めたWをGPSログの2点間の時間差Tで割ることにより求められます。そして最終的には駆動系の伝達効率0.95で割ることによって補正します。つまりパワーPは
P=W/T/0.95
で求められます。これがGPSログの1区間における瞬間的なパワーであり、それを1kmくらいの長い区間にわたって平均してやれば平均パワーを求めることができるわけです。
この手法の限界
ここでは純粋に物理的な計算によりライダーの出力パワーを求めましたが、実際にパワーメーターを持っていませんので結果が正しいかどうかは検証できていません。ただGPSの精度が十分高ければ、それほど間違った値が出ることはないと思います。物理法則に例外はないからです。
ただし空気抵抗は近似式によって求めているため、特に平地では誤差が大きくなる可能性が考えらます。逆に上り坂では空気抵抗はほぼ無視できて標高差だけで決まるため、かなり正確に求められるはずです。
そして最も重大な問題は、風の影響を全く考慮していないということです。自転車乗りならよく知っているように、向かい風と追い風では天と地ほどの違いがあります。同じスピードで走るにも必要なパワーは全然違ってくるでしょう。しかしGPSログからはある瞬間にどんな風が吹いていたかを知ることは不可能なのです。それこそ風速センサーを取り付けるしか方法はありません。
しかし向かい風があれば追い風もあるわけで、コース全体を平均すればある程度相殺されるのではないかとも考えられます。したがって瞬間的なパワーとしてはあまり信頼できませんが、平均パワーであればそこそこ参考になる値を出せるのではないかと考えています。
次回はヒルクライムに限定して簡単にパワーを見積もる方法について解説します。